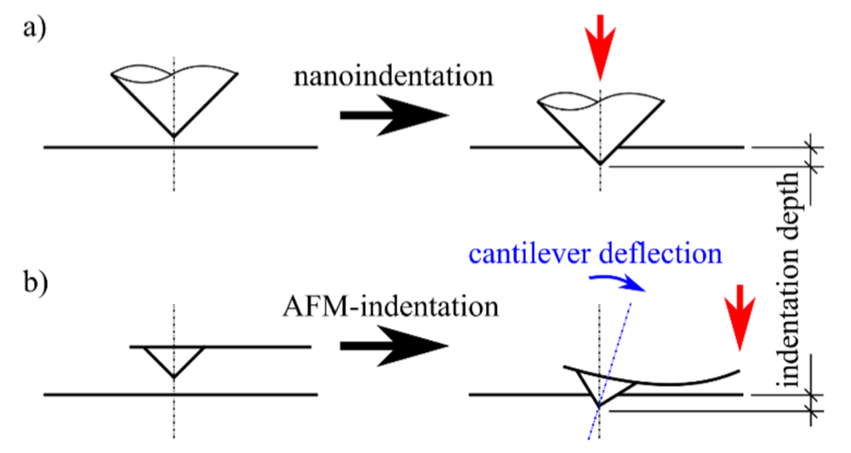
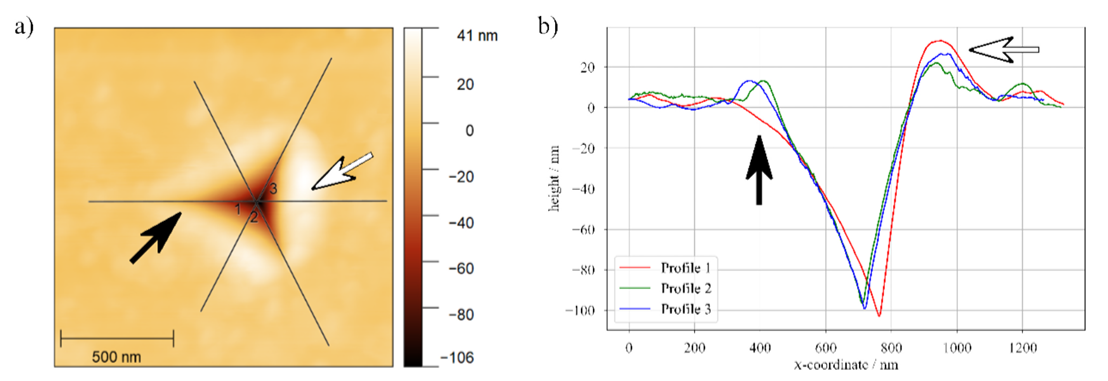
在設計新型元件與應用時,掌握材料的微觀力學性質至關重要。這不僅涵蓋標準材料與應用(例如金屬材料中奈米結構或薄膜的量測),也包括非標準材料,如軟性聚合物、生物樣品,以及歷史/文化遺產文物。於微尺度下量測材料硬度與楊氏模數的一種可行方法為奈米壓痕(nanoindentation)。然而,若希望在不依賴昂貴的電子顯微鏡原位量測的情況下,達到更小的量測尺度並同時具備優異的成像能力,則可採用原子力顯微鏡(AFM)壓痕技術。
雖然已有多項研究探討 AFM 壓痕,但目前結果分析多半僅採用兩種主要方法——赫茲接觸力學(Hertzian contact mechanics)與 Sneddon 理論,且通常與球形壓頭結合使用。然而,若改用尖銳的金字塔形壓頭並結合 Oliver–Pharr 分析法,則可帶來額外優勢,例如統一深壓痕與淺壓痕的分析,以及實現更為局部化的變形量測。
本文提出一種新的方法,將改良後的 Oliver–Pharr 方法與透過樣品硬度進行的壓頭面積校正相結合,並引入一個隨懸臂偏移量變化的參數 β。該方法在軟材料(環氧樹脂–矽、聚碳酸酯)以及硬材料(熔融石英與鎳)上的驗證結果顯示出相當具前景的表現。
材料科學的一個不可否認的核心目標,是研究既有材料的性質,以進一步加以改良,或根據先前的研究成果設計與合成新材料。這一目標促使了各種新材料表徵方法的發展,使人們能夠可靠地檢驗並改進材料本身及其應用。然而,隨著材料研究與製程技術的不斷進步,材料所涉及的長度尺度範圍與應用領域也持續擴展,這同時要求實驗技術必須相應提升,才能跟上新發現的步伐。本研究的目的在於量測材料於微米至奈米尺度下的機械性質,並改進目前最先進的方法。
材料的機械性質,特別是楊氏模數E與硬度H,可依不同尺度透過多種方法進行量測。在宏觀至中觀尺度上,可利用標準拉伸或壓縮試驗來量測材料的彈性性質,以及其降伏與加工硬化行為。為了評估材料硬度及相關的塑性變形,可採用微硬度測試方法,例如適用於硬材料的洛氏(Rockwell)、布氏(Brinell)、努氏(Knoop)或維氏(Vickers)測試,以及適用於軟材料的硬度計(Durometer)測試 [2]。然而,當尺度縮小至微觀層級時,便難以直接沿用宏觀量測的方法。
儘管如此,鑒於各類應用中裝置小型化的廣泛需求,仍有必要以高度局部化的方式了解材料的機械性質,以便理解其在實際使用過程中的表現,並支援尺寸小於一毫米之樣品的製造流程。目前,拉伸測試可延伸為微拉伸試棒,壓縮測試可微型化為微柱壓縮試驗,彎曲試驗亦可微型化為微懸臂梁。然而,這些方法普遍需要繁瑣且耗時的樣品製備,通常依賴成本高昂的聚焦離子束(FIB)技術,且並非適用於所有材料。
此外,微硬度測試僅能提供材料硬度資訊,且其壓痕深度通常約為 100 µm,對於真正的材料微觀表徵而言仍屬過大尺度。例如,對金屬材料中單一晶粒或生物樣品(如植物細胞)的表徵,往往需要介於 10 至 100 nm 的壓痕深度。為了將硬度測試尺度進一步縮小,發展出了儀器化奈米壓痕(instrumented nanoindentation)技術,其可利用完整的載荷–位移曲線,在壓痕深度低於 1 µm 的情況下,同時量測材料的彈性與塑性性質。
在奈米壓痕中,量測是透過將尖銳壓頭壓入樣品中進行,藉此量測材料中一個極小體積的機械反應,並同時連續記錄壓頭尖端的位移與其所受到的反作用力 [12]。最早對於球形壓頭的載荷–位移曲線分析,係基於赫茲接觸力學模型 [13,14]。其後,Sneddon 將該方法延伸至錐–球形壓頭 [15,16],再由 Oliver 與 Pharr 建立了載荷–位移曲線、壓頭幾何形狀、量測硬度H與約化楊氏模數Er之間的完整關係:
其中Pmax為壓痕過程中施加的最大力,Ac為在指定接觸深度時壓頭與樣品之間的接觸面積,而S則為卸載段載荷–位移曲線(約 99%–40% 區間)的初始斜率。約化彈性模數Er與樣品的真實楊氏模數E及泊松比v,以及壓頭的楊氏模數Etip與泊松比v_tip之間的關係為 :
除了 Oliver–Pharr(O–P)方法外,尚有其他方式可利用相同的奈米壓痕數據來獲得材料的機械性質。基於能量與位移關係的方法,透過分析奈米壓痕曲線下方的面積,萃取彈性能與塑性能,並將其與約化彈性模數及硬度相關聯。然而,這類方法需對不同材料作出多項假設,且高度依賴複雜的理論與經驗模型。在硬度量測方面,可採用名義硬度(nominal hardness)或塑性硬度(plastic hardness)方法,透過數值與經驗校正,將系統的能量平衡與材料硬度相連結。儘管這些方法具有一定實用性,但它們高度依賴複雜的校正程序,包含多個以經驗或數值方式獲得的參數,且通常未被整合於標準奈米壓痕儀中。相較之下,O–P 方法因其應用直接、對多種材料皆能提供經驗證的高精度結果,且除表面拋光外無需特殊樣品製備,而被廣泛應用於商用與客製化奈米壓痕系統中。因此,在本研究中,O–P 方法將作為奈米壓痕結果分析的主要方法。
近年來,奈米壓痕技術亦被延伸至原子力顯微鏡(AFM)領域。AFM 的主要用途是在奈米尺度下,透過在樣品表面掃描一個安裝於振動懸臂上的微小探針,於接觸、間歇接觸或非接觸模式下,利用原子尺度的吸引與排斥力來表徵表面結構與性質。這項原本以成像為主的技術,已被拓展至多個領域,其中之一即是透過壓痕進行材料機械性質的量測。AFM 本質上使用一個裝載於懸臂上的探針與樣品接觸,並藉由雷射量測懸臂的偏移,以高精度量測探針位移。透過將探針壓入材料,並已知懸臂的彎曲剛性(彈簧常數),即可萃取完整的載荷–位移曲線,其原理與奈米壓痕相似,但施加力更小、量測精度更高。目前,多數商用設備在分析載荷–位移曲線時,主要採用兩種方法:適用於淺層彈性壓痕的赫茲接觸理論,以及適用於深層彈塑性壓痕的 Sneddon 模型。然而,這兩種方法皆包含多項假設與簡化。赫茲模型假設壓痕完全為彈性變形,這在實際情況中並非總能成立;此外,該模型需要已知探針半徑,因而較適合半徑大且鈍的球形探針,其尺寸易於量測,且在多次壓痕後不易改變。Sneddon 模型則要求足夠深的壓痕(以避免探針半徑效應),並假設探針為幾何已知的錐–球形,這些條件都會為結果分析引入不確定性。
雖然 AFM 奈米壓痕已成功應用於多種材料與領域——包括軟性聚合物、天然纖維材料 、生物樣品以及硬材料如硬質聚合物、金屬–有機骨架材料 或礦物——但對於結果分析方法本身,除基本或延伸的赫茲與 Sneddon 模型,或直接使用 O–P 方法外,仍鮮少有深入探討,且多半仍使用鈍或球形探針基於上述研究,O–P 方法結合 AFM 壓痕的整體有效性尚無法被確認,因此,O–P 方法不應以與標準奈米壓痕相同的方式直接套用於 AFM。
若能結合 O–P 方法與 AFM 優異的成像能力,以及精準的壓痕定位技術,將可大幅提升材料微米與奈米尺度機械性質的表徵能力。此一結合方式可引入尖銳金字塔形壓頭的優勢,例如對變形區域的高度局部化控制,以及相較於大型球形壓頭更小的壓痕面積,同時避免赫茲與 Sneddon 方法所帶來的額外誤差。本文即展示了 O–P 方法在多種材料上的應用,並揭示了在使用安裝於可變形懸臂上的尖銳探針,對 AFM 奈米壓痕結果(載荷–位移曲線)進行分析時,對現有最先進方法所需進行的關鍵修正。